- نوآوری ها
- مقاله در مورد استفاده از PCI
- معاملۀ سبد تجاری
بهینه سازی سبد از طریق روش PQM (بخش 1)
بحران جهانی اقتصاد که در سال 2008 رخ داد تمامی بخش های فعالیت اقتصادی را بدون استثناء متاثر کرد. این بحران بطور مستقیم و غیرمستقیم فعالیت کسب و کار و شرکت ها تحت تاثیر قرار داد اما سطح این تاثیر همه جا به یک میزان نبود. این حقیقت باعث شد تا فرصت های وسیعی برای پیدا کرد استراتژی های سرمایه گذاری بر اساس اختلافات موجود مثلاً در واکنش بلندمدت قیمت ها در بازار سهام در همان عامل سیستماتیک پدید آید.
در این مقاله تلاش خواهیم کرد تا سبدی را مثال بزنیم که بطور آماری و گرافیکی بازتاب دهندۀ امکان ایجاد یک استراتژی سرمایه گذاری موفق بر مبنای اختلافات در رفتار بلندمدت بازار سهام است. در این راستا، 22 سهم از سهام بزرگترین و نقدشونده ترین شرکت های بورسی ایالات متحده متعلق به بخش های مختلف اقتصادی را انتخاب کرده ایم. با استفاده از نظریۀ مدرن سبد تجاری، مبانی تنوع خطر risk diversification و همچنین روش قیمت دهی سبد (PQM)، تلاش خواهیم کرد تا دارائی های مان را به دو گروه سبد "خوب" و سبد "بد" تقسیم کنیم.
سبد "خوب" دارائی های با وزن مثبت را شامل می شود که کاندید خرید هستند. سبد "بد" سهامی را شامل می شود که بر اساس تحلیل های مان باید فروخته شوند. تمامی تحلیل ها بر اساس بسته شدن نمودار ماهیانۀ قیمت طی چهار سال ( 50 ماه) اخیر صورت می گیرند. ترکیب دارائی ها (22 سهم) که برای ایجاد یک سبد انتخاب شده اند، با ذکر نام اختصاری، نام شرکت های شان و بخش های اقتصادی مربوطه شان در ذیل ارائه می گردند:
جدول 1: اسامی شرکت ها و بخش های اقتصادی سهام انتخاب شده
| # | Ticker | Company | Sector |
| 1 | AA | AlcoaInc | BasicMaterials |
| 2 | AXP | AmericanExpressCompany | Financials |
| 3 | BA | BoeingCompany | Industrials |
| 4 | DD | DupontCompany | BasicMaterials |
| 5 | DIS | WaltDisneyCompany | CyclicalConsumerGoods&Services |
| 6 | GE | GeneralElectricCorporation | Industrials |
| 7 | HD | HomeDepotInc | CyclicalConsumerGoods&Services |
| 8 | HON | HoneywellInternationalInc | Industrials |
| 9 | HPQ | Hewlett-PackardCompany | Technology |
| 10 | IBM | InternationalBusinessMachineCorp | Technology |
| 11 | INTC | IntelCorporation | Technology |
| 12 | JNJ | Johnson&Johnson | Healthcare |
| 13 | JPM | JP MorganChase&Company | Financials |
| 14 | KO | Coca-ColaCompany | ConsumerNon-Cyclicals |
| 15 | MCD | McDonaldsCorporation | CyclicalConsumerGoods&Services |
| 16 | MRK | MerckCoInc | Healthcare |
| 17 | MSFT | MicrosoftCorporation | Technology |
| 18 | PFE | PfizerInc | Healthcare |
| 19 | T | AT&T | Telecommunication |
| 20 | VZ | VerizonCommunicationsInc | Telecommunication |
| 21 | WMT | Wal-MartStoresInc | CyclicalConsumerGoods&Services |
| 22 | XOM | ExxonMobilCorporation | Energy |
ما بر مبنای داده های ماهیانه، میزان میانگین بازده، انحراف معیار بازده و نسخۀ ساده شدۀ نرخ برای هر مجموعه داده را محاسبه می کنیم.
نتایج محاسبات میانگین بازده های ماهیانه و انحراف معیار در جدول زیر نمایش داده شده اند:
| Asset | MeanReturn | StandardDeviation | Asset | MeanReturn | StandardDeviation |
| AA | 0.31% | 10.60% | JNJ | 1.01% | 3.76% |
| AXP | 3.32% | 10.96% | JPM | 1.27% | 9.05% |
| BA | 1.99% | 6.96% | KO | 1.31% | 4.16% |
| DD | 1.81% | 7.90% | MCD | 1.22% | 3.68% |
| DIS | 2.58% | 6.54% | MRK | 1.11% | 5.28% |
| GE | 1.64% | 8.48% | MSFT | 1.20% | 6.67% |
| HD | 2.33% | 6.41% | PFE | 1.54% | 4.85% |
| HON | 2.05% | 6.40% | T | 0.78% | 4.16% |
| HPQ | -0.80% | 10.36% | VZ | 1.27% | 4.83% |
| IBM | 1.49% | 4.27% | WMT | 0.83% | 4.17% |
| INTC | 0.92% | 6.59% | XOM | 0.58% | 4.65% |
بعلاوه، می توانیم برای هر دارائی نسخۀ ساده شده ای از نرخ شارپه (Sharpe - نسبت بازدهی به ریسک) را محاسبه کنیم. این نرخ حاصل تقسیم بازده به انحراف معیار است و بازده را در هر واحد از ریسک نشان می دهد. این ضرایب تاثیر می توانند راهنماهای خوبی برای تحلیل گران باشند تا بتوانند تاثیر استراتژی سرمایه گذاری را تعیین کنند. ضرایب تاثیر حاصل شده در نموداری نشان داده می شوند:
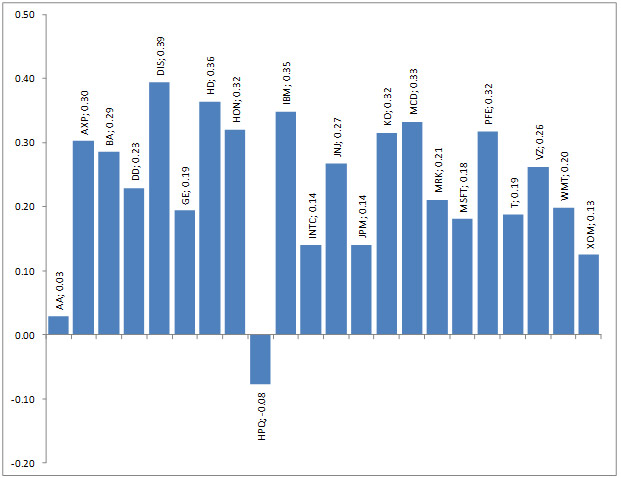
مرحلۀ بعدی تحلیل، شامل پیدا کردن وزن ضرایب تاثیر بهینه برای هر دارائی و ایجاد یک سبد سهام می شود. معیار بهینه بودن سبد بر اساس نرخ شارپه (Sharpe)، پارامتر بازده و یا انحراف معیار سنجیده می شود. در اینجا، معیار بهینه بودن در واقع همان حداکثر بازدۀ ممکن برای سبد خواهد بود که در سطوح انحراف معیار قابل دسترس است نه بالاتر از میانگین انحراف معیار برای نمونۀ ارائه داده شده از 22 سهم. میانگین انحراف معیار برای 22 سهم برابر است با 6.40% و خواستۀ ما این است که ریسک سبدمان بطور میانگین بیشتر از دارائی های اصلی اش نباید. برای محاسبۀ ضرایب تاثیر وزن، به کوواریانس دارائی ها نیز نیاز داریم که سطح ارتباط متقابل بین هر دارائی را تعیین می کند.
روند بهینۀ سازی وزن (ضمن دارا بودن دو محدودیت : حداکثر انحراف استاندارد سبد (6.40%) و جمع نهایی وزن ها که باید 100% باشد) ما را به راه حل زیر هدایت می کند که بازده سبد را به حداکثر می رساند:
| Asset | Weight | Asset | Weight |
| AA | -70.27% | JNJ | 21.59% |
| AXP | 8.97% | JPM | -31.82% |
| BA | -4.39% | KO | 29.55% |
| DD | -22.00% | MCD | -15.80% |
| DIS | 88.08% | MRK | -5.98% |
| GE | -41.55% | MSFT | 51.73% |
| HD | 37.01% | PFE | 39.28% |
| HON | 145.66% | T | -96.14% |
| HPQ | -43.92% | VZ | 81.77% |
| IBM | 152.36% | WMT | -56.03% |
| INTC | -39.34% | XOM | -128.76% |
از آنجائیکه در احتمال فروش دارائی ها محدودیت اعمال نکرده ایم، راه حل هم منوط به وزن منفی و به وزن مثبت می شود. دارائی های با اوزان مثبت، سبد "خوب" و دارائی های با اوزان منفی ، سبد "بد" نامیده می شوند. اکنون دارائی های را بر اساس طبقه بندی جدیدشان دوباره دسته بندی می کنیم:
| GoodPortfolio | BadPortfolio |
| Asset | Weight | Asset | Weight |
| AXP | 8.97% | AA | -70.27% |
| DIS | 88.08% | BA | -4.39% |
| HD | 37.01% | DD | -22.00% |
| HON | 145.66% | GE | -41.55% |
| IBM | 152.36% | HPQ | -43.92% |
| JNJ | 21.59% | INTC | -39.34% |
| KO | 29.55% | JPM | -31.82% |
| MSFT | 51.73% | MCD | -15.80% |
| PFE | 39.28% | MRK | -5.98% |
| VZ | 81.77% | T | -96.14% |
| WMT | -56.03% | ||
| XOM | -128.76% |
تعداد دارائی های "بد" اندکی از دارائی های "خوب" بیشتر است. هرچند، صرف دادن یک صفت به آنها نمی تواند از اهمیت شان بکاهد. آنچنان که بعداً شاهد خواهیم بود، این دو گروه از دارائی فقط زمانی می توانند مؤثرترین عملکردشان را نشان دهد که باهم باشند. چراکه برای شرکت هایی که به یک بخش اقتصادی تعلق دارند، نمی توانیم یک الگوی خاص برای شرکت هایی که به یک سبد خاص وارد می شوند را برجسته کنیم. شرکت ها، نمایندۀ بخش های کاملاً متفاوت هستند و در هر دو سبد حضور دارند.
در اینجا نمودارهای مربوط به سبد های "خوب" و "بد" را بطور جداگانه نشان می دهیم. ما از روش قیمت دهی سبد (PQM) استفاده خواهیم کرد که در ترمینال تجاری تحلیلی نت ترید ایکس (NetTradeX) بکار رفته است. از سبد "خوب"، 10 دارایی را انتخاب و ارزش اش را به دلار آمریکا بیان می کنیم چراکه خواهان مشاهدۀ ارزش مطلق اش هستیم. برای انجام این کار، همزمان با توجه به نسبت، برای هر دارائی وزن ضریب تاثیر را طبق آنچه قبلاً در راه حل سبد بهینه حاصل شده بود، به دلار آمریکا نشان می دهیم. به عنوان مثال، برای سهام AXP مبلغ 987 دلار و برای سهام VZ حجم 8177 دلار را وارد می کنیم. علی رغم اینکه حجم با دلار تنظیم شده است نه به درصد، تاثیری روی شکل منحنی سبد نمی گذارد بلکه فقط روی هماهنگی ها تاثیر می گذارد. نمودار به شکل زیر است:
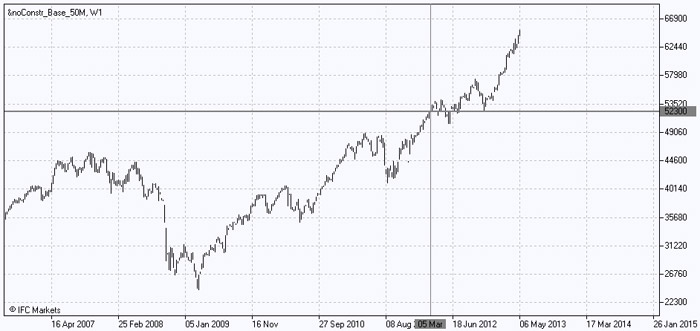
بطور کلی، یک ساختار گذشته نگر رو به رشد در اختیار داریم. از ابتدای ژانویۀ 2009 تاکنون ارزش سبد "خوب" 2.5 برابر افزایش پیدا کرده است اما باید به این نکته هم اشاره کنیم که ارزش همین سبد در سال 2008 بطور چشمگیری کاهش پیدا کرد. این سبد همچنین در ابتدای مارس 2012 ارزش این سبد حول و حوش 52,300 دلار در نوسان بود. این حقیقت در آینده به ما کمک خواهد کرد تا بتواند حرکات سبد ترکیبی را مطالعه کنیم.
به همین نحو، یک سبد "بد" شامل 12 دارائی ایجاد می کنیم و حجم های مرتبط را به دلار آمریکا نشان می دهیم. نوسانات گذشته نگرش در نمودار نمایش داده می شوند:
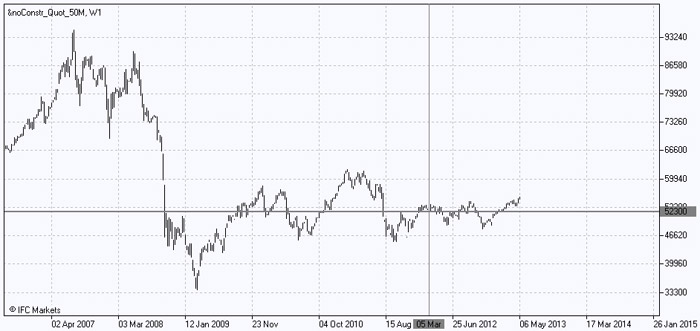
سبد "بد" به خوبی نشان می دهد که چرا "بد" نامگذاری شده است. این سبد بطور قابل توجهی در ارتباط با بازدهی دریافت شده نسبت به سبد "خوب" ضعیف تر است که از کاهش سه برابری ارزش در سال 2008 و رشد های اندکی در پی آن، مشخص است. بعلاوه، لازم به یادآوری است که ارزش سبد "بد" در ابتدای مارس 2012 حول و حوش 52,300 دلار نوسان داشت.
سرانجام، یک سبد ترکیبی ایجاد خواهیم کرد که شامل دارائی های "بد" و "خوب" می شود که اوزان شان در خلال بهینه سازی به دست آمده اند. توجه داشته باشید که اوزان منفی مرتبط به فروش دارائی هستند. هنگام ایجاد یک سبد در پلت فرم تحلیلی تجاری نت ترید ایکس (NetTradeX)، دارائی های دارای اوزان مثبت در بخش پایۀ سبد ترکیبی قرار می گیرند در حالیکه دارائی های با اوزان فروشی در بخش مظنه قرار می گیرند. به عبارت دیگر، ما بطور مشروط دارائی های سبد "خوب" را می خرید و دارائی های سبد "بد" را می فروشیم. این دو کار بازتاب دهندۀ ماهیت روش PQM هستند. نتیجه یک ضریب تاثیر است که ارزش سبد اولی (در این مورد، سبد "خوب") را به واحد سبد دومی (سبد "بد") بازتاب می هد و نمودار نیز این امکان را برای مان میسر می کند که تغییراتش را در خلال تمام دورۀ زمانی دنبال کنیم:
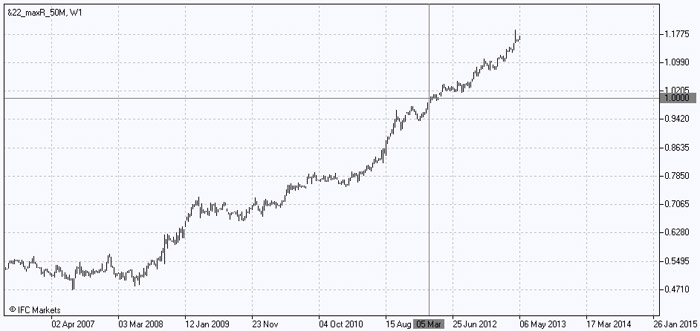
بطور معجزه آسایی یک ساختار رو به رشد از سبد ترکیبی به دست می آوریم که از هرگونه افت قابل توجهی در سال 2008 به دور مانده و در دورۀ زمانی پس از بحران، رشدی مدام، مستمر و آرام داشته است. بعلاوه، شاهد این هستیم که پس از بحران سال 2008 یک رشد چشمگیر آغاز شده است که بازتاب دهندۀ درجات مختلف واکنش های دارائی به یک عامل جهانی هستند و طبق آنچه نمودار نشان می دهد اهمیت این عامل و واکنش های دارائی ها به آن تاکنون بالا هستند.
اندیکاتورهای راندمانِ مقداری، مربوط به سبد ترکیب شده در جدول زیر نشان داده شده اند:
| Return | 7.52% |
| StDev | 6.40% |
| Sharpe | 1.18 |
به کمک پوزیشن های فروش به راحتی می توان تعیین کرد که بازدۀ سبد بسیار بیشتر از بازدهی های فردی معلوم شدۀ هر دارائی است (حداکثر میانگین بازدهی 3.32% بود). انحراف استاندارد بازده 6.40% بود که با حد تعیین شده در ارتباط است. در نسخۀ ساده شدۀ ضریب تاثیر شارپه (Sharpe) اش برای سبد (1.18) که بازتاب دهندۀ اثرش است، بسیار بیشتر از نرخ های متعلق به هر کدام از 22 سهم (حداثر ضریب تاثیر شارپه برای نمونۀ سهام 0.39 بود) است.
چگونه می توان این رشد قدرتمند سبد ترکیبی را توضیح داد؟ بای پاسخ به این پرسش، باید سبد های "خوب" و "بد" را جداگانه بسنجیم. بهینه کردن وزن این امکان را به ما می دهد که در مورد دارائی های مورد نظرمان ترکیب پوزیشن های خرید و فروش را پیدا کنیم که به خوبی با استراتژی سرمایه گذاران در ارتباط خواهد بود. با استفاده از روش PQM و مدلش در ترمینال نت ترید ایکس (NetTradeX) قادر خواهیم بود تا حرکات هر دو سبد بطور جداگانه و بطور ترکیب شده باهم را دنبال کنیم.
تحلیل رفتار سبدها نشان می دهد که در خلال وخیم ترین بحران که در سال 2008 رخ داد، سبد "خوب" کمتر از سبد "بد" متحمل ضرر شد. در دورۀ پس از بحران نیز ثابت شد که رشد سبد اول برجسته تر از رشد سبد دوم بوده است. با ترکیب این دو عامل، به یک ساختار رشد مستمر دست پیدا می کنیم. از آنجائیکه رشد سبد ترکیبی از سال 2008 (قبل از آنکه سبد ترکیبی وارد روندی خنثی شود) آغاز شد، فرض را بر این می گیریم که این سال یک نقطۀ بازگشت بوده است که طی آن دارائی ها واکنش های مختلفی به برخی از عوامل سیستماتیک نشان دادند. توجه داشته باشید که ارزش سبد "بد" پیش از مارس 2012 از ارزش سبد "خوب" بیشتر بوده است یعنی ضریب تاثیر نسخه های ترکیبی زیر 1 بود. هرچند، در مارس 2012 ارزش قطعی شان برابر شد و ضریب تاثیر برابر با 1 شد. پس از آن لازم شد که واحد های سبد "بد" بیشتر و بیشتر یک واحد از سبد "خوب" را خریداری کنند.

